| Elektronika MK-61/52
|
 |
 |
 |
 |
 |
 |

| Caractéristiques | MK-Compiler | Calculators 3000 | Modèle MK-52 | Module ROM BRP-3 (Maths) | Module ROM BRP-4 (jeux) | Tests de vitesse |
Calculatrice RPN avec

|
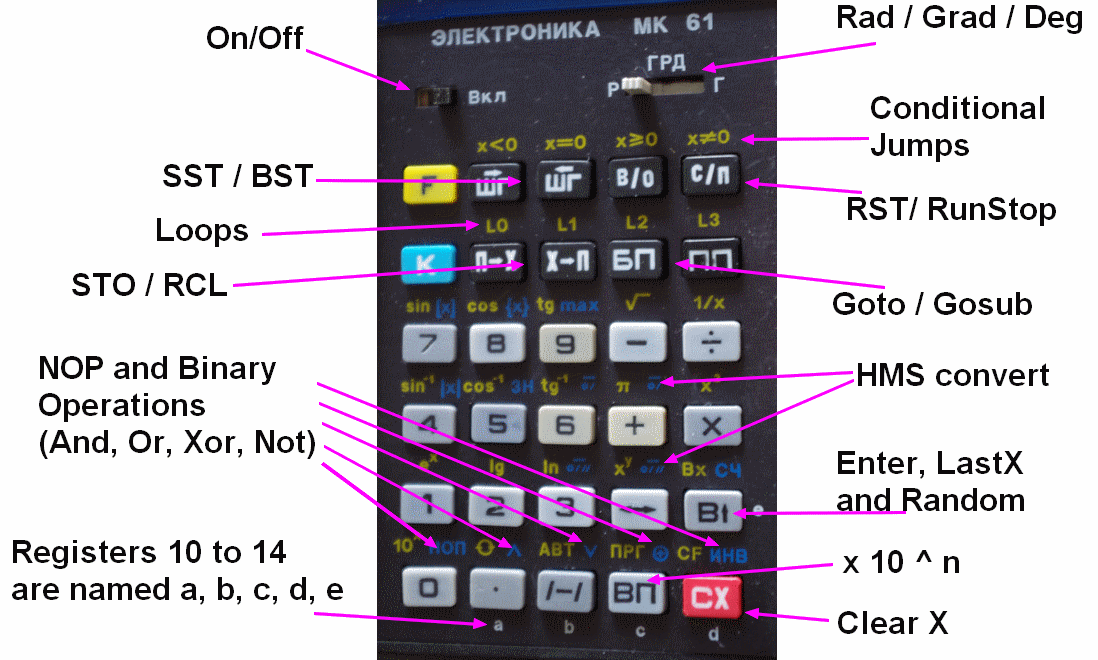 |
| Forensic Test de précision sur les fonctions scientifiques, on calcule arcsin(arccos(arctan(tan(cos(sin(9))))))en degrés. Résultat: 9.0881454. L'idéal serait 9 ! |
Hebdogiciel20 =0 =1 2 FOR 0 SQR NEXT FOR 1 X^2 NEXT STOPRésultat: 1.6889469 L'idéal serait 2 ! |
J'ai écrit un petit compilateur pour Windows qui :
NEW : recrée un fichier source à partir d'un C3. NEW : recrée un fichier source à partir des codes Hexadécimaux tapés au clavier. |
 |
; NEWTON method for equations ; solves f(x)=0 ; function is programmed at label f(x), it receives x on the stack ; it can use the whole stack and registers 4-9 and b-d ; set precision into register "e" (0.01 for example) ; in the X register, put a first guess of the solution and RUN. ; it returns the solution. ; you can start again with new parameters (precision or starting x) ; usage: store error in register e (example 0.01 STO e) ; go to first step ( B/0) ; key in the first x value and RUN. #c3 1 ; auto save to C3 file #reg e error #reg a x #reg 0 delta #reg 1 h #reg 2 fxh #reg 3 fx DO =x $1e-4 =delta REPEAT @x @delta * IF(x=0)THEN @delta ENDIF =h ; h=0.0001x or 0.0001 if x=0 @x + GOSUB f(x) =fxh ; calculates f(x+h) @x GOSUB f(x) =fx ; calculates f(x) @h * @fx @ fxh - / ; calculates dx = hf(x)/(f(x)-f(x+h)) = -f(x)/f'(x) ENTER sum x ; new x = x + dx x<>y abs @error - ; abs(dx) - error UNTIL(x<0) ; stop if <0 (if abs(dx) < error) @x ; display x STOP LOOP f(x): RTN |
Step | Code | Keys ------------------------ 000 | 4A | STO a 001 | 01 | 1 002 | 0C | EE 003 | 04 | 4 004 | 0B | /-/ 005 | 40 | STO 0 006 | 6A | RCL a 007 | 60 | RCL 0 008 | 12 | * 009 | 5E | F X=0 010 | 12 | 1 2 011 | 60 | RCL 0 012 | 41 | STO 1 013 | 6A | RCL a 014 | 10 | + 015 | 53 | GOSUB 016 | 42 | 4 2 017 | 42 | STO 2 018 | 6A | RCL a 019 | 53 | GOSUB 020 | 42 | 4 2 021 | 43 | STO 3 022 | 61 | RCL 1 023 | 12 | * 024 | 63 | RCL 3 025 | 62 | RCL 2 026 | 11 | - 027 | 13 | / 028 | 0E | ENTER 029 | 6A | RCL a 030 | 10 | + 031 | 4A | STO a 032 | 14 | X<>Y 033 | 31 | K ABS 034 | 6E | RCL e 035 | 11 | - 036 | 5C | F X<0 037 | 06 | 0 6 038 | 6A | RCL a 039 | 50 | STOP 040 | 51 | GOTO 041 | 00 | 0 0 042 | 52 | RTN ------------------------ Addr | Name ------------------------ 042 | F(X) ------------------------ Reg | Name ------------------------ 0 | DELTA 1 | H 2 | FXH 3 | FX a | X e | ERROR ------------------------ |
|
Eugene Troitskiy est l'auteur du superbe Calculators 3000.
Il s'agit d'un émulateur de toute une gamme de calculatrices Russes (une vingtaine). On y retrouve bien-sur la MK-61 et le modèle
légèrement supérieur, la MK-52.
J'ai fait la traduction française du logiciel, les gens rétifs à toute langue étrangère pourront donc profiter un peu de l'émulateur sans trop se noyer. Dans le compilateur, avec la directive #C3 on peut obtenir un fichier C3 directement utilisable avec Calculators 3000. Il suffit ensuite de le charger dans l'émulateur avec l'option "Ouvrir avec la calculatrice courante *.C3". 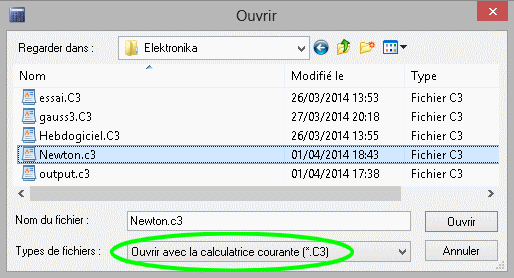
Le fichier C3 généré ressembe à ceci: group Document end MachineFileName = "MK61.cfg" group Machine group ProgramMemory Size = 105 Data = 4A010C040B406A60125E1260416A105342426A5342436112636211130E 6A104A14316E115C066A505100520000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000 0000000000000000000000 end end |
 |
C'est un modèle amélioré de la MK-61 avec en particulier:
Lisez cet article très précis sur l'utilisation de l'Eprom, un grand merci à Alexandre Dumont pour la traduction du russe vers l'anglais! |

|
| Exemple avec la factorielle: | Fichier compilé: | Effacement de la mémoire: | Sauvegarde: | Chargement: |
|---|---|---|---|---|
#reg 0 n
DO
=n
1
FOR n
@n *
NEXT
STOP
LOOP |
Step | Code | Keys ------------------------ 000 | 40 | STO 0 001 | 01 | 1 002 | 60 | RCL 0 003 | 12 | * 004 | 5D | F L0 005 | 02 | 0 2 006 | 50 | STOP 007 | 51 | GOTO 008 | 00 | 0 0 ------------------------ Reg | Name ------------------------ 0 | N ------------------------ |
Le programme nécessite 9 pas, nous allons donc préparer la place pour 9 octets dans l'EEPROM à partir
de l'adresse zéro. Pour cela, on bascule l'interrupeur sur CLEAR.1000009 A↑ ↑↓ L'adresse est construite ainsi: 1ssssbb avec
|
On tape ensuite le programme! (en effet, la fonction CLEAR a le mauvais goût d'effacer aussi
la RAM). Une fois le programme entré, pour sauvegarder, on bascule l'interrupteur sur SAVE, l'autre sur PROGRAM et 1000009 A↑ ↑↓ Votre programme a encore disparu, la fonction SAVE efface aussi la RAM... |
Pour récupérer finalement votre programme, même après extinction de la machine, placez l'interrupteur sur LOAD(*),
assurez vous l'autre est toujours sur PROGRAM, et:
1000009 A↑ ↑↓ Ca y est, il est revenu en mémoire ! |
1001820 A↑ ↑↓En effet, 9 octets déjà pris, c'est 18 nibbles (demi-octet!), et à partir de ce 18è nibble, vous voulez 20 octets.
Il s'agit d'un module contenant 60 programmes mathématiques enfichable dans le MK-52. Parmi les thèmes on trouve:
Télécharger le manuel du module BRP-3 |
 |
| Système à deux inconnues | Remplissage des données | Résultats |
|---|---|---|
Le programme 5 de la banque 1 résout le système suivant:
a.x + b.y = c a'.x + b'.y = c'Allumez le module, sur la banque 1, interrupteurs en position LOAD et PROGRAM, puis tapez: 1047635 A↑ ↑↓L'adresse est fournie par le manuel, le programme est maintenant utilisable. |
Entrez les données dans les registres:
|
On remet le pointeur programme à zéro avec в/О puis on éxécute avec
С/П. En retour vous avez à l'affichage la valeur de y, puis avec ↔ la valeur de x (également dans les registres 1 et 2), le déterminant étant dans le registre 3. Si l'affichage signale une erreur (ЕГГОГ), c'est que le déterminant est nul et qu'il n'y a pas une solution unique. |
Il s'agit d'un module contenant 54 programmes enfichable dans le MK-52. Parmi les thèmes on trouve:
Télécharger le manuel du module BRP-4 |
 |
Dans ce jeu, on doit aligner trois points selon le schéma suivant: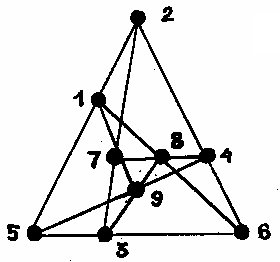
|
Allumez le module, sur la banque 2, interrupteurs en position LOAD et PROGRAM, puis tapez:
1176498 A↑ ↑↓L'adresse est fournie par le manuel, le programme est maintenant utilisable. Pour l'initialisation on stocke 77 dans Rd et on lance avec в/О puis С/П |
Le jeu renvoit la valeur du point qu'il veut occuper: il prend le 1!
Je mets en retour la valeur du point que je prends, exemple 8, puis С/П. On poursuit le jeu ainsi de suite. Si il affiche 77, c'est qu'il a gagné! Avec la touche ↔ vous verrez son dernier coup. |
| Le programme | Résultats | Conclusion |
|---|---|---|
STEP KEY n + n+1 GOTO n+2 nLa pile contenant 1-1-1-0, ainsi on réalise un comptage de 1 en 1 à partir de zéro. L'exécution du programme se fait pendant 60 secondes, on stoppe la machine et on lit le compteur. Le test a été réalisé aux pas 0, 8, 16 etc... |
 |
La MK-61 est 15% plus rapide que la MK-52. Le numéro du pas a une influence significative sur la vitesse d'exécution. Vers le pas 100, elle n'est plus que 73% de celle du pas zéro. Les pas de 0 à 31 permettent une vitesse maximale. |
| Le programme | Résultats | Conclusion |
|---|---|---|
Prog i Prog reference STEP KEY STEP KEY 00 RCL i 00 NOP 01 STO i 01 NOP 02 L3 02 L3 03 00 03 00 04 STOP 04 STOPLe registre i contenant PI, le registre 3 contenant 50 pour une boucle de 1 à 50. J'ai réalisé un programme de référence en remplaçant RCL/STO par deux NOP (no-operation). Les temps donnés sont l'écart entre ces deux programmes. J'ai réalisé ce test en utilisant les registres i=0, 4, 8, 12. |
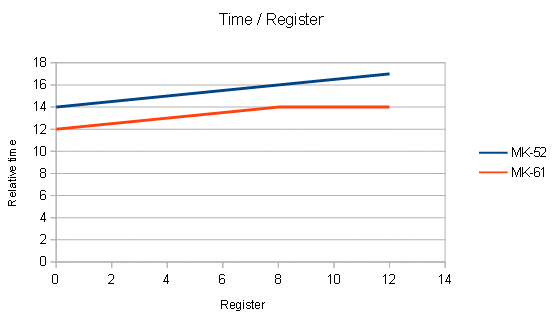 |
Même si les écarts ne sont pas spectaculaires, plus le numéro de registre est bas, plus l'exécution est rapide. |