Elektronika MK-61/52

Specifications

RPN Calculator with

Four numbers stack X, Y, Z, T
15 registers (0-9 and a-e)
display 8+2 fluo
105 program steps
the ram is cleared when powered off...
precision is limited to what is displayed
interesting functions

random numbers
binary operations
HMS conversions

Good programming capabilities

loops
4 conditional tests
indirect addressing
sub-programs

Precision Tests

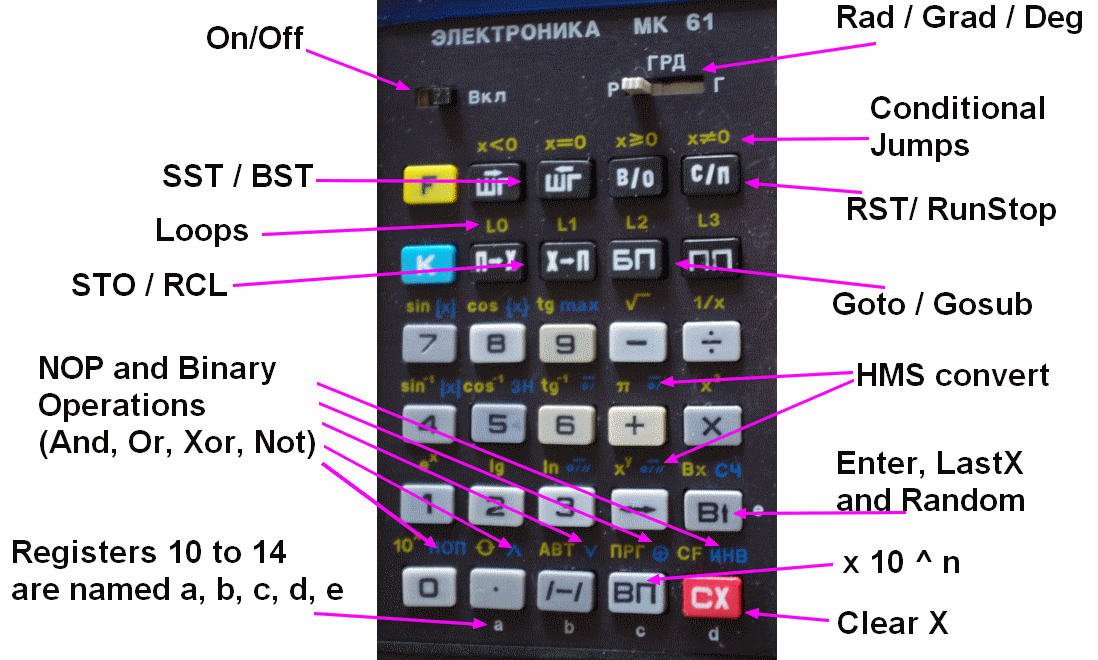Forensic

On scientific functions, calculate in degrees:

arcsin(arccos(arctan(tan(cos(sin(9))))))

Result: 9.0881454.

The exact value is 9 !

Hebdogiciel

20 =0 =1
2
FOR 0 SQR NEXT
FOR 1 X^2 NEXT
STOP

Result: 1.6889469

The exact value is 2 !

MK-Compiler

I wrote a little compiler for Windows that :

allows you to write programs with a high level language
calculates for you the addresses for jumps
outputs a list with opcodes and key for the program
can be linked to the emulator Calculators 3000.

Download MK-Compiler V1.02 (april 2014)

NEW : recreate a source file from a C3 program file.
NEW : recreate a source file from a serie of hex codes.

Here is an example with the Newton's method to solve equations f(x)=0

Source file in input for MK-Compiler

LST file output by the compiler

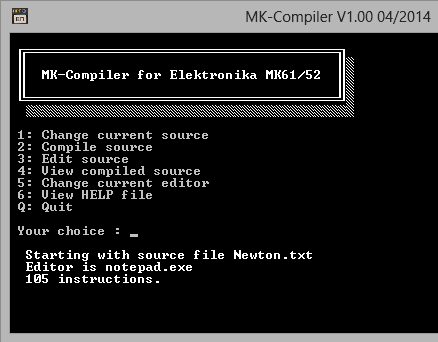; NEWTON method for equations

; solves f(x)=0
; function is programmed at label f(x), it receives x on the stack
; it can use the whole stack and registers 4-9 and b-d

; set precision into register "e" (0.01 for example)
; in the X register, put a first guess of the solution and RUN.

; it returns the solution.
; you can start again with new parameters (precision or starting x)

; usage: store error in register e (example 0.01 STO e)
; go to first step ( B/0)
; key in the first x value and RUN.

#c3 1		; auto save to C3 file

#reg e error
#reg a x
#reg 0 delta
#reg 1 h
#reg 2 fxh
#reg 3 fx

DO
	=x
	$1e-4 =delta
	REPEAT
		@x @delta *
		IF(x=0)THEN
			@delta
		ENDIF
		=h			; h=0.0001x or 0.0001 if x=0
		@x + GOSUB f(x) =fxh	; calculates f(x+h)
		@x GOSUB f(x) =fx	; calculates f(x)
		@h *
		@fx @ fxh - /		; calculates dx = hf(x)/(f(x)-f(x+h)) = -f(x)/f'(x)
		ENTER
		sum x			; new x = x + dx
		x<>y abs
		@error -		; abs(dx) - error
	UNTIL(x<0)			; stop if <0 (if abs(dx) < error)
	@x				; display x
	STOP
LOOP

f(x):
RTN

  Step | Code | Keys
------------------------
  000  |  4A  | STO a
  001  |  01  | 1
  002  |  0C  | EE
  003  |  04  | 4
  004  |  0B  | /-/
  005  |  40  | STO 0
  006  |  6A  | RCL a
  007  |  60  | RCL 0
  008  |  12  | * 
  009  |  5E  | F X=0 
  010  |  12  | 1 2
  011  |  60  | RCL 0
  012  |  41  | STO 1
  013  |  6A  | RCL a
  014  |  10  | + 
  015  |  53  | GOSUB 
  016  |  42  | 4 2
  017  |  42  | STO 2
  018  |  6A  | RCL a
  019  |  53  | GOSUB 
  020  |  42  | 4 2
  021  |  43  | STO 3
  022  |  61  | RCL 1
  023  |  12  | * 
  024  |  63  | RCL 3
  025  |  62  | RCL 2
  026  |  11  | - 
  027  |  13  | / 
  028  |  0E  | ENTER 
  029  |  6A  | RCL a
  030  |  10  | + 
  031  |  4A  | STO a
  032  |  14  | X<>Y 
  033  |  31  | K ABS 
  034  |  6E  | RCL e
  035  |  11  | - 
  036  |  5C  | F X<0 
  037  |  06  | 0 6
  038  |  6A  | RCL a
  039  |  50  | STOP 
  040  |  51  | GOTO 
  041  |  00  | 0 0
  042  |  52  | RTN 
------------------------

  Addr |  Name
------------------------
  042  |  F(X)
------------------------

  Reg  |  Name
------------------------
   0   |  DELTA
   1   |  H
   2   |  FXH
   3   |  FX
   a   |  X
   e   |  ERROR
------------------------

Calculators 3000

Eugene Troitskiy is the author of the great Calculators 3000. This emulator gives you access to a large field of russian calculators (20 of them!). Among them, the MK-61 and the enhanced MK-52.

Link with MK-Compiler

When compiling a program, you can use the #C3 directive to get a C3 file loadable by Calculators 3000. You just have to load it with the option "Open with current calculator".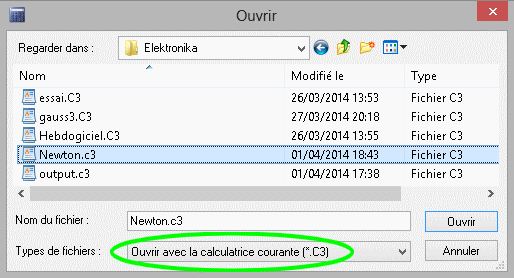

MK-Compiler generates a C3 file that looks like this:

group Document
end
MachineFileName = "MK61.cfg"
group Machine
group ProgramMemory
Size = 105
Data = 4A010C040B406A60125E1260416A105342426A5342436112636211130E
6A104A14316E115C066A505100520000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000
end
end

Enhanced MK-52

It is an enhanced model, similar to the MK-61, but with the following:

One 512 bytes EEPROM (1024 nibbles) to save registers and programs
One module ROM port to use preprogrammed stuff

One bad point, this calculator seems to be 15% slower than the MK-61...

Read this highly detailed article about the Eprom usage, a big thank to Alexandre Dumont for translating from russian to english !

Let's save a little program.

The factorial example:	Compiled file:	Clearing memory:	Saving:	Loading:
#reg 0 n DO =n 1 FOR n @n * NEXT STOP LOOP	Step \| Code \| Keys ------------------------ 000 \| 40 \| STO 0 001 \| 01 \| 1 002 \| 60 \| RCL 0 003 \| 12 \| * 004 \| 5D \| F L0 005 \| 02 \| 0 2 006 \| 50 \| STOP 007 \| 51 \| GOTO 008 \| 00 \| 0 0 ------------------------ Reg \| Name ------------------------ 0 \| N ------------------------	The program uses 9 steps, so you have to prepare 9 free bytes in the EEPROM, let's say from address zero. To do that, put the switch on CLEAR. 1000009 A↑ ↑↓ The address is defined this way: 1ssssbb with 1 necessary digit, but non significant ssss start nibble in memory bb number of bytes concerned The key A↑ sets the address, and the key ↑↓ executes the operation according to the switch (CLEAR in this example)	Then, you key in the program! Don't do it before as the CLEAR function erases both EEPROM and RAM ! Once it is entered, to save it, put the switches on SAVE and on PROGRAM and: 1000009 A↑ ↑↓ Once again, your program has desappeared, the SAVE function clears the RAM...	To get your program back into RAM, even after a power off, put the switch on LOAD(*), the other being on PROGRAM, and: 1000009 A↑ ↑↓ This time, it came back to RAM !

Next address...

Let's imagine that you want to keep this 9 bytes factorial program in the EEPROM. If then, you have a second 20 bytes program to save, the new address will be:

1001820 A↑  ↑↓

Explanations: 9 bytes occupied are 18 nibbles (half-bytes!), and then, from that 18th nibble, you want to use 20 bytes.

(*) Switch OFF the ROM module, when you have one, else, the copy will be performed from ROM and not from the EEPROM !

ROM Module BRP-3

This is a module containing 60 maths programs that you plug into the MK-52. Among them, you'll find:

Equation solver
Integration
Differential equations
Matrix
Complex numbers

I translated the manual into French (apart five programs marked as INCOMPLET).

Download french manual for ROM Module BRP-3

Each program has its own ROM address that you must know to copy it from ROM to RAM.

Let's use a little program.

Simultaneous equations	Entering data	Results
The program 5 of bank 1 solves this system: a.x + b.y = c a'.x + b'.y = c' Switch the module ON, set bank to 1, switches in position LOAD and PROGRAM, then type: 1047635 A↑ ↑↓ This address comes from the user's manual, the program is now ready in RAM.	Enter the data into the registers: a, b and c into the registers 7, 8 and 9 a', b' and c' into the registers 4, 5 and 6 The digits layout on the keyboard justify the choice of the registers.	Put the program pointer to zero with в/О and run it with С/П. Upon return, the display gives you the y value, with ↔ you get the x value (also in registers 1 and 2), the determinant is in register 3. If the display tells you ЕГГОГ, then the determinant is nul and no unique solution can be found.

ROM Module BRP-4 (Games)

This is a ROM module containing 54 programs that you can plug into the MK-52. Among them, you'll find:

Health/Anthropometry/Food
Games
Financial tools
Metric conversions

I translated the manual into French (apart nine programs marked as INCOMPLET).

Download french manual for ROM Module BRP-4

Every program is defined by a ROM address that you'll find in the manual to load it from ROM to RAM.

Example with the Triangular Tic Tac Toe.

In this game you must align three points using this diagram :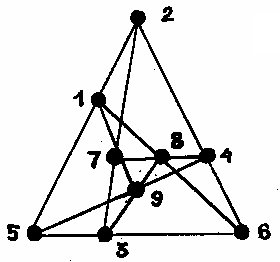

Switch the module ON, select bank 2, switches in positions LOAD and PROGRAM, then type:

1176498 A↑  ↑↓

The address comes from the manual, now you can use the program.

Initialize it with 77 into register Rd and run it with в/О then С/П

The games returns the first position taken by the computer: it takes the 1!

Now, I type the position I want, let's say 8, and then С/П.

The game goes on this way. If 77 is displayed, the computer has won and typing ↔ you'll see its last position taken.

Speed testings

I wanted to know wether the position in memory of a program changes the execution time or not.

The program	Results	Conclusion
STEP KEY n + n+1 GOTO n+2 n The stack contains 1-1-1-0, so the program counts one by one starting from zero. The program is run during 60 seconds, then stopped and I just have to read the current counter value. The test has been performed at steps 0, 8, 16 etc...		The MK-61 is 15% faster than the MK-52. The step number has a significant influence on the excution speed. When at step 100, the speed is only 73% compared to the one at step zero. Step from 0 to 31 give the maximal speed.

I wanted to know wether the position in memory of a register changes the execution time or not.

The program	Results	Conclusion
Prog i Prog reference STEP KEY STEP KEY 00 RCL i 00 NOP 01 STO i 01 NOP 02 L3 02 L3 03 00 03 00 04 STOP 04 STOP Register i contains PI, register 3 contains 50 for a loop 1-50. I wrote a reference program replacing RCL/STO with two NOP (no-operation). The execution times are the differences between the two versions. The test has been performed using registers i=0, 4, 8, 12.		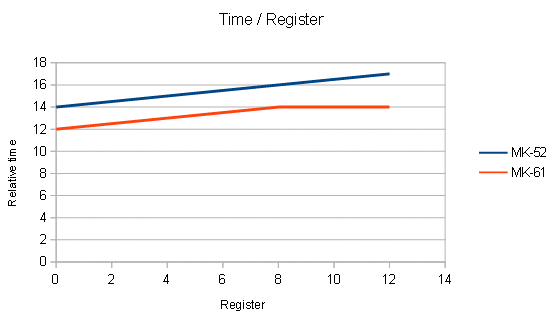Even if differences are not spectacular, the lower, the faster!

Conclusion, to speed up your program:

The most used registers must have the lowest numbers.
The most used parts of a program must be located at the lowest step numbers.