|
Mais sa grande puissance vient de ses capacités en programmation! Non seulement on accède à toutes les fonctions mathématiques, mais le TOS est largement couvert et donne accès aux appels VDI, AES, GEMDOS, BIOS et XBIOS. On peut également ajouter des routines en assembleur! Très bien programmé sous GEM, cette version de fin 1991 tourne encore sur un TT avec une carte graphique et en couleur. Il refuse d'être exécuté en TT Ram... Dommage pour le gain de puissance et de place ! Note : j'ai fait la traduction en anglais à partir de la version 1.20 en allemand. J'ai également la version 1.21 mais qui se montre instable lors de la programmation en particulier. |

|
In addition to this base, it comes with a complete programming system. Not only you have access to all mathematical functions, but you can use every system call such as the AES, VDI, GEMDOS, BIOS and XBIOS. You can even call machine routines! Very cleanly programmed under GEM, this old piece of software still runs on a TT with graphic card and colors. It just refuses to run from the TT Ram, too bad for the extra power and memory ! Note : I made the english translation of version 1.20, the original was in german. I have version 1.21 but this last is unstable when programmed. |
Résolvons un problème pour parcourir quelques aspects de RIEMANN II. Un ouvrier fait se croiser deux échelles de 2m et 3m dans un couloir. Le point d'intersection se trouve à 1m du sol. On demande la largeur du couloir (valeur A). |
 |
Lest's solve a problem to step through some of the features of RIEMANN II. A worker places two scales of 2m and 3m in a corridor. The point where they cross is located at 1m above the ground. Can we evaluate the width of this corridor? (value A). |
Avec le théorème de Pythagore et la fonction SOLVE. |
 |
Using the Pythagorean theorem and the SOLVE function. |
Je clique sur la solution positive et elle est copiée vers la pile (voir ligne d'info verte de la fenêtre) |
 |
I clic on the positive solution and it is copied to the stack (see the green info line of the window) |
 |
||
Puis avec F10 je peux recopier ces formules et les éditer pour affecter chaque solution à X puis à Y. |
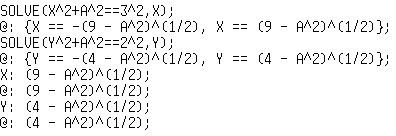 |
Then using F10 I can copy back the formulas and edit the lines ti assign the results to X and Y. |
C'est l'affichage par défaut des formules, comme on le ferait à la main (comparez les deux dernières lignes, l'une avec et l'autre sans). Pour mon problème du jour, je l'ai désactivé car il n'est pas pratique pour recopier et éditer les formules. |
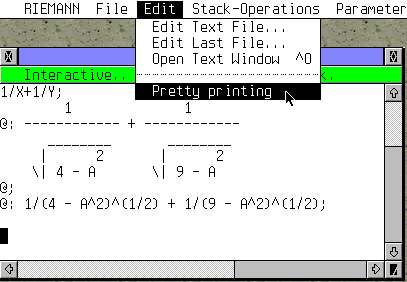 |
It's the default display format as you would write on a paper by hand (compare the last two lines, one with pretty printing ON and the other OFF). For the current problem, it is not convenient for copying and editing, so I disabled it. |
La hauteur de 1m est la demi moyenne harmonique de X et Y. Je l'écris avec "==" pour une équation (sinon c'est un test logique). La dernière réponse s'appelle toujours "@", j'utilise celle facilité dans SOLVE pour résoudre l'équation, mais...? |
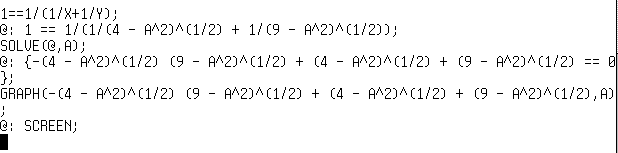 |
The 1m height is the half of the harmonic mean of X and Y. So I write it using "==" for an equation (else, it's a logical test). The last answer is called "@", so I use this shortcut with SOLVE to solve the equation for A. But.... |
...RIEMANN ne trouve pas de solution algébrique. Il a simplifié l'équation. J'utilise donc cette fonction de A pour obtenir un graphe. Une solution apparaît entre 1 et 2! Le graphe, sur un TT en 640x480x16bits, est obtenu en 2 secondes environ. |
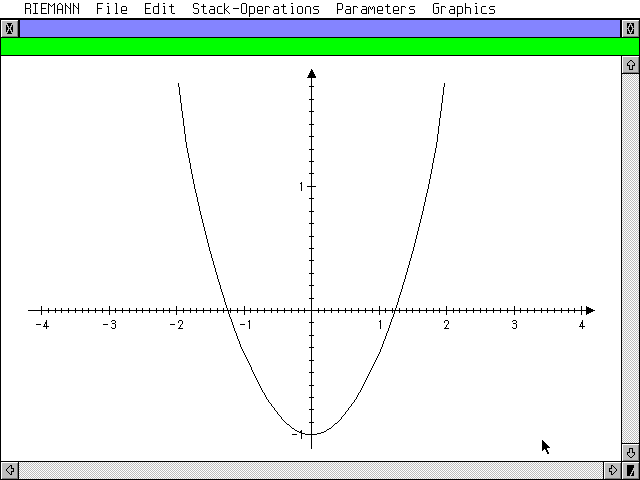 |
...RIEMANN can't find any algebraic solution. The equation was simplified. I use this last to get a graph according to A. A solution appears between 1 and 2 ! The graph, on a TT with 640x480x16bits display, is drawn in about 2 seconds. |
Je n'ai pas encore tout exploré, d'autant que le mode AUTO me donne satisfaction. On remarquera la possibilité d'avoir une échelle logarithmique et celle d'envoyer le graphe vers l'imprimante ou un fichier Metafile (présence de GDOS obligatoire dans ces deux cas). |
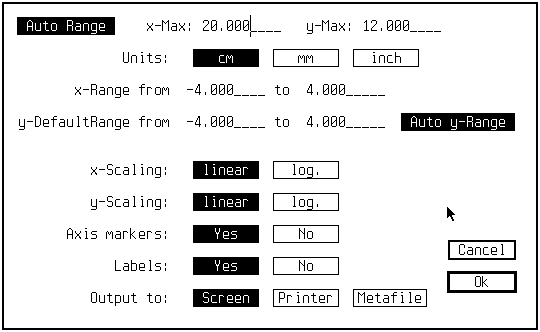 |
I didn't change any setting as the AUTO mode satisfies me for now. Let's underline some points: you can get logarithmic scales and print to the Printer or a Metafile (GDOS is required for the last two). |
On va profiter des possibilités de programmation afin d'ajouter la méthode de Newton à RIEMANN qu'on appellera ainsi: NEWTON(F,X,init,précision) F étant la fonction de la variable X. Init la valeur de départ et précision, la précision souhaitée. |
 |
Let's use the programming features to add to RIEMANN the Newton's method for finding the roots of an equation.We'll call it this way: NEWTON(F,X,init,precision) F is the function of the variable X. Init is the starting value for X and precision, the precision you want to acheive. |
Note: la fonction est déclarée avec 8 paramètres, mais on n'en utilise que quatre lors de l'appel, les autres sont les variables locales.
|
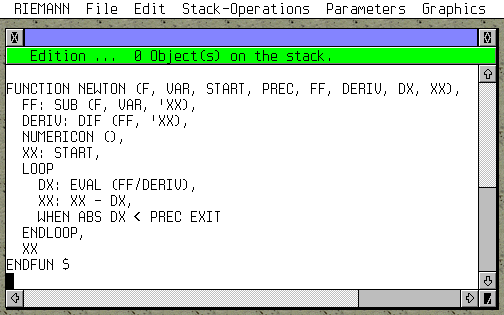 |
Note: the function has 8 parameters but we only use four of them when calling. The other are the local variables.
|
Reste à appeler NEWTON avec notre equation, variable A, valeur de départ 1 et une précision de 0,0001 afin d'avoir un chiffre correct pour les millimètres. Après environ une seconde et demi, on obtient A ≈ 1,231 m |
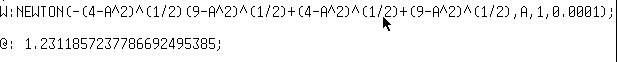 |
We just call NEWTON with our equation, variable A, init value of 1 and a precision of 0.0001 to get a correct digit for millimeters. After about 1 second and a half, RIEMANN returns A ≈ 1,231 m |
la fonction pour tracer un graphe 3D de la forme Z= f (X,Y) est très simple! |
 |
the function to draw a 3D-Graph of the form Z= f (X,Y) is really easy! |
Les surfaces sont dessinées avec les traits cachés. Le dessous est tramé gris, le dessus les éclairé et les ombres sont rendues avec différents niveaux de vert ou bleu. Le tracé s'effectue sur TT en 640x480x16bits en une dizaine de secondes. |
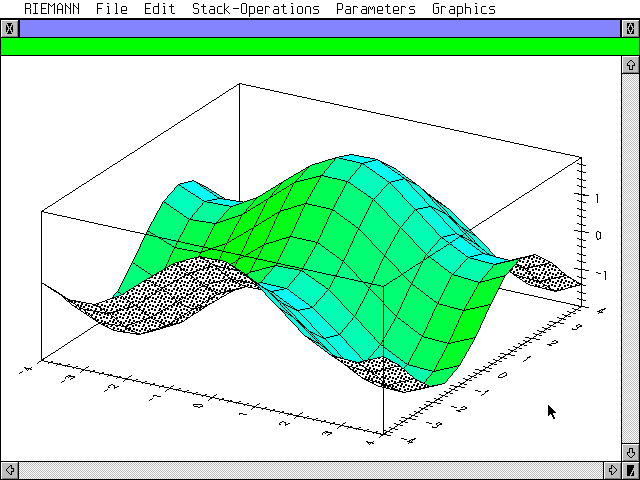 |
The surface is drawn with hidden lines. The bottom is grayed and the top is enlightened rendering the shadows with different levels of blue and green. The graph is drawn on a TT with 640x480x16bits screen in about 10 seconds. |
On retrouve à peu près les réglages de la 2D. A noter, pour obtenir une sortie imprimante ou metafile, le réglage est celui de la fenêtre 2D. C'est l'option LIGHTING qui permet la coloration de la surface, sinon, elle reste blanche. |
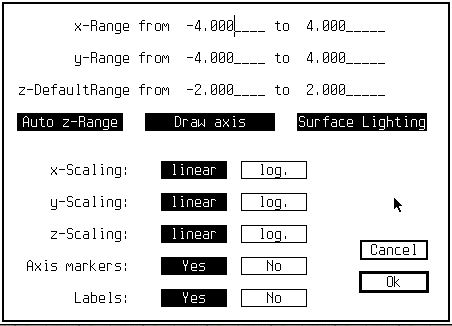 |
The settings are similar to the 2D window. Note that if you want an output to printer or metafile, you have to set it on the 2D window. The LIGHTING options allows the surface to be painted, else it remains white. |
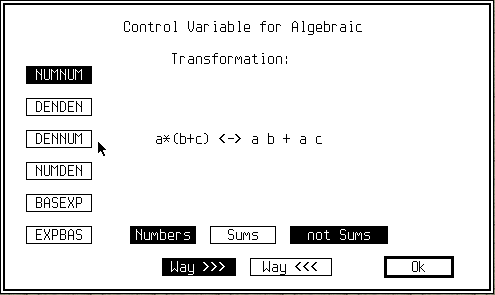
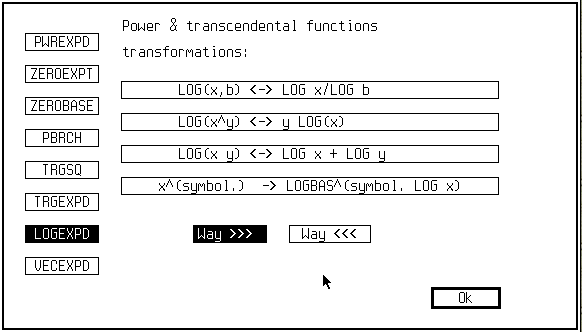
Ce menu donne acès à de très nombreux réglages pour controler le comportement du système algébrique de RIEMANN |
It gives access to a huge number of internal settings to control precisely the behaviour of RIEMANN's algebraic system |
|
 |
 |
 |
Pour l'exportation vers un fichier TeX, il suffit de charger PRTEX.RIE (le pack TeX) via l'entrée du menu "Load Text File". Une fois ce programme chargé, il faut de définir la variable TEXFILENAME pour indiquer le fichier de sortie. Ensuite, pour exporter une ligne "résultat" (celles commençant par "@:"), il vous suffit de positionner le curseur dessus et d'utiliser la combinaison de touches Ctrl+*. Chaque formule est ajoutée au fichier de sortie. |
To export to TeX, you have to load the file PRTEX.RIE (the TeX package) through the menu entry "Load text file". Once loaded, you have to set the variable TEXFILENAME to the file name you want to use. Then, for each result line you want to save (one starting with "@:"), place the cursor on it and use the key combination Ctrl+*. Each line will be added to the specified file. |
|
Comme les égyptiens, je voudrais fabriquer un cylindre contenant mon savoir. Sa hauteur sera e ≈ 2,718 m et sa surface totale sera π ≈ 3,1416 m² Quel doit être le RAYON ? SOLUTION:
RAYON ≈ 0,173 m |
 |
As the Egyptians, I want to build a cylinder containing my knowledge. Its height will be e ≈ 2,718 m and its area will be π ≈ 3,1416 m². What RADIUS should I use ? SOLUTION:
RADIUS ≈ 0,173 m |
Pour chaque ligne du problème ci-dessus, j'ai envoyé le résultat avec Ctrl+* vers le fichier de sortie CYLINDER.TEX. Ce dernier doit être traité par un compilateur TeX. Vous pouvez, par exemple, utiliser ce site Quicklatex.com dans lequel vous copiez-collez le fichier généré par RIEMANN et vous obtenez l'image ci-contre : |
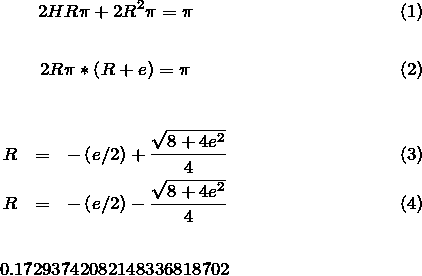 |
For each line of the problem above, I sent the result to the output file CYLINDER.TEX using Ctrl+*. This last must be managed by a TeX compiler. As an example, you can use Quicklatex.com on line and just copy/paste the file generated by RIEMANN and you'll get this image: |
Pour être utilisé avec le pack C-TEX sous TOS, il manque quelques instructions. J'ai donc modifié PRTEX.RIE pour ajouter deux nouveaux appels.
|
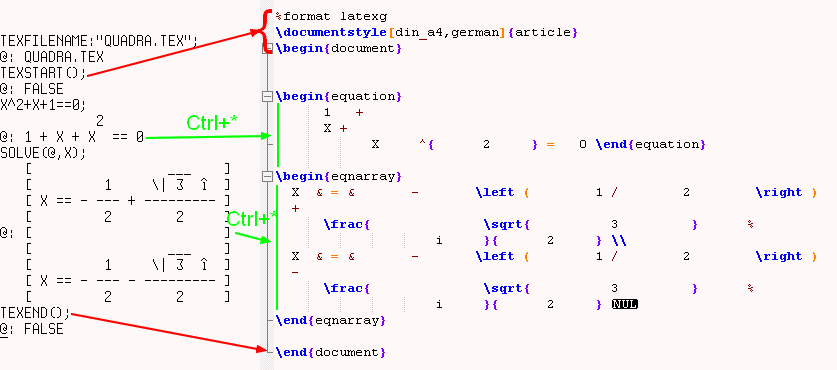 |
To be loaded by C-TEK under TOS, some instructions are missing in the TeK file. That's why I modified PRTEX.RIE and added two more calls.
|
Il reste à charger notre fichier TEX dans C-TEX et de demander sa compilation: menu WORK, item TEX. Le fichier DVI est prévisualisé sur Atari et vous pouvez l'utiliser sur toute plateforme. |
 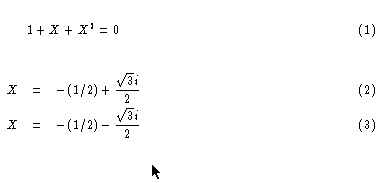 |
Then, just load that TEX file into C-TEX and compile it: menu WORK, item TEX. The DVI file is previewed on the Atari and saved on disk. You can then view it on any platform. |
De même que pour la résolution d'équation, l'intégration se fait de manière algébrique exacte. L'appel est DEFINT (pour intégrale définie losqu'on connait les bornes). Mais, si il n'y a pas de solution, il nous faut encore une méthode numérique. Voici, ci contre, mon adaptation de la méthode de GAUSS à trois points. Elle accepte 4 ou 5 paramètres.
|
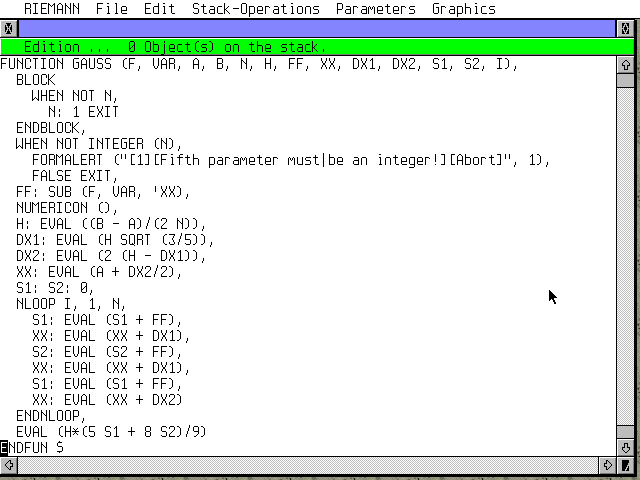 |
As for solving equations, the integration in RIEMANN is algebraic, giving an exact answer. The call is DEFINT (for definite integral). But if there is no answer, we must, once again, use a numerical method. Here is my adaptation of the GAUSS method with three points. In input, you can give 4 or three parameters :
|
D'abord on revient au mode algébrique et je définis deux expressions TEST et TEST2. Je calcule leurs intégrales exactes: 13/6 et -1/4. Pour la première, ma méthode donne le bon résultat: 13/6 ≈ 2.166.., en fait cette méthode donne la résultat exact pour tout polynôme jusqu'au degré 5 inclus. Pour la seconde, le résultat est proche de -1/4, mais pas exact. J'augmente alors le nombre d'intervalles à 10, puis à 100 et le résultat devient de plus en plus précis. |
 |
First, let's enter the algebraic mode and define two expressions TEST and TEST2. Then, using DEFINT, I get the exact values of their integral: 13/6 and -1/4. For the first one, the GAUSS method is perfect as 13/6 ≈ 2.166.., in fact, this method gives an exact answer for every polynomial expression up to the 5th degree. For the second one, the answer is close to -1/4, but not no good. So you can increase the number of intervalls, for example 10 or 100 and you can see the answer getting closer to the exact one. |
En passant, c'est l'occasion d'en parler. Si vous utilisez régulièrement les même programmes: pour moi c'est PRTEX, NEWTON et GAUSS (mes deux méthodes numériques et l'impression TeX), on peut se passer du chargement à chaque lancement en sauvagardant la mémoire dans un fichier SYS. Ensuite, on peut récupérer cet état à chaque session. Cela conserve également vos variables et le contenu da la pile. Pour enregistrer en plus le contenu de la fenêtre d'édition, il faut en passer par "Save Editor Buffer". |
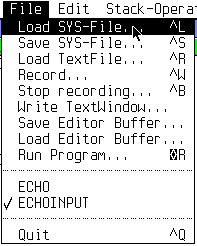 |
By the way... if, as I do, you have to load everytime the same programs to get your personal environment, you can simplify this by saving the whole memory to a SYS file. Then, at every session, you can reload it and you'll get your programs back! For me, it's PRTEX, NEWTON and GAUSS that are automatically included in my SYS file. This also saves your variables and the content of the stack. To save the content of the editing window, you can add a call to "Save editor buffer". |
RIEMANN est une évolution de muMATH (qui servira également de base à DERIVE sur PC et calculatrices Texas Instruments). Ce premier programme datant du début des années 80 est écrit dans un dialecte de LISP. On en retrouve des aspects dans certains appels de RIEMANN concernant la gestion des LISTES justement. On peut penser qu'il a été écrit en LISP sur Atari, mais rien ne permet de l'affirmer, mais quand même, ça sent l'héritage direct! Par exemple, l'expression 3+X² est représentée intérieurement par la liste ( + 3 ( ^ X 2 ) ). Faisons donc un peu de LISP... |
RIEMANN is an evolution of muMATH (that will also give birth to DERIVE on PC and Texas Instruments calculators). This first program from the early 80's was written using a LISP dialect. Some aspects of LISP remain in RIEMANN, for example the LIST managment. There's a signifient probability that RIEMANN was written in LISP, but nothing allows me to assert that, but... the legacy seems obvious! For example, the expression 3+X² is represented internally by the list ( + 3 ( ^ X 2 ) ). Let's do some LISP... | 2
|
 |
|
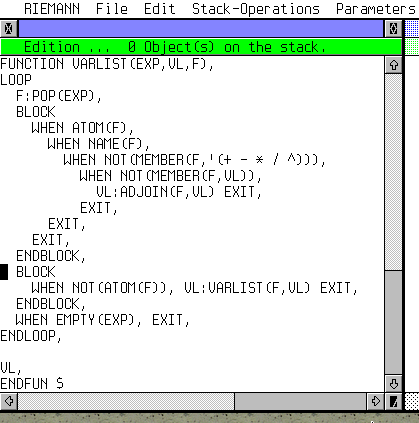
On essaye VARLIST sur l'expression X²+3X-2, le résultat est une liste d'un seul élément (X). La longueur du résultat est 1. Puis sur l'expression A/(5+X*Y), le résultat est la liste (Y X A), de longueur 3. Quelques limites de cette fonction incomplète, voyez la ligne suivante, la fonction COS est considérée comme une variable! Il faudrait que la liste des opérateurs à écarter soit complétée de toutes les fonctions mathématiques! De même avec la valeur PI, elle est aussi vue comme une variable. Note : les expressions mathématiques sont terminées par ";" alors que les expressions liste doivent être terminées par un "&" pour un affichage correct. |
 |
Let's try VARLIST on the expression X²+3X-2, the result is a one-element list (X). The lenght of the list is 1. Then on the expression A/(5+X*Y), the result is the list (Y X A), whose lenght is 3. Some limits to this uncomplete function. Have a look at the next call, the COS function is seen as a variable. Every math function should be added to the operator list! The same with PI, its value is seen as a variable. Note : the terminator for evaluating maths expressions is ";", and the one for list expression is "&". |
(*) certains systèmes évaluent systématiquement xª par EXP ( a LN (x) ). Ce qui rend le calcul presque indépendant de la valeur de l'exposant. |
 |
(*) some systems always replace xª with EXP ( a LN (x) ). This makes the calculation independant from the exponent. |
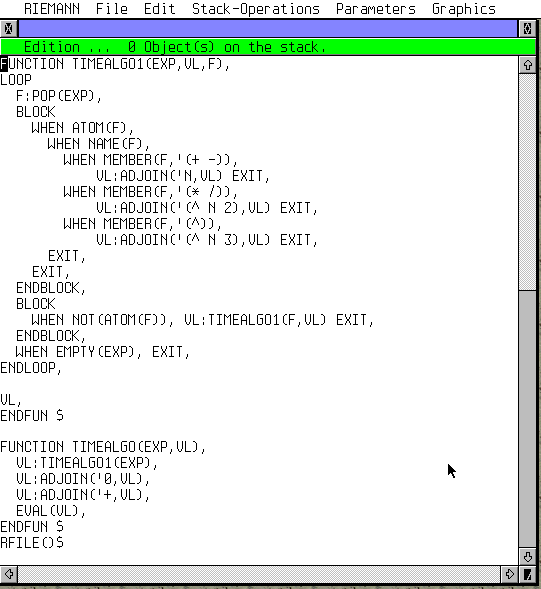
A gauche : Comparons TIMEALGO sur deux expressions égales: 1 + X + X² et 1 + X * ( 1 + X ). Les deux renvoient N + N³. Il se trouve que RIEMANN évalue et simplifie l'expression passée en paramètre. Observez qu'en donnant l'expression factorisée, il renvoie l'expression développée et réduite. Il faut aller dans le menu Parameters et décocher toutes les transformations algébriques automatiques. Par ailleurs, on devrait avoir 2N + N³ car il y a deux additions. Sauf que de manière interne, l'addition de plusieurs termes se résume à une seule liste, donc "+" n'apparaît qu'une fois. A droite : Avec de meilleurs réglages, j'affecte à S le temps de calcul de l'expression 1 + X + X², c'est à dire S = N + N³. Et j'affecte à F le temps de calcul de l'expression 1 + X * ( 1 + X ), c'est à dire F = 2N + N². Je crée un graphe vide avec 0 comme expression. Puis je change de couleur et ajoute le graphe de S, puis encore une autre couleur et j'ajoute le graphe de F. On peut ainsi comparer les croissances des deux calculs selon la précision souhaitée grâce au graphique. (DIVOUT permet de simplifier le quotient S/F si on veut la croissance comparée de manière analytique). |
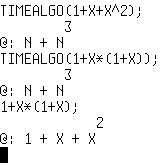  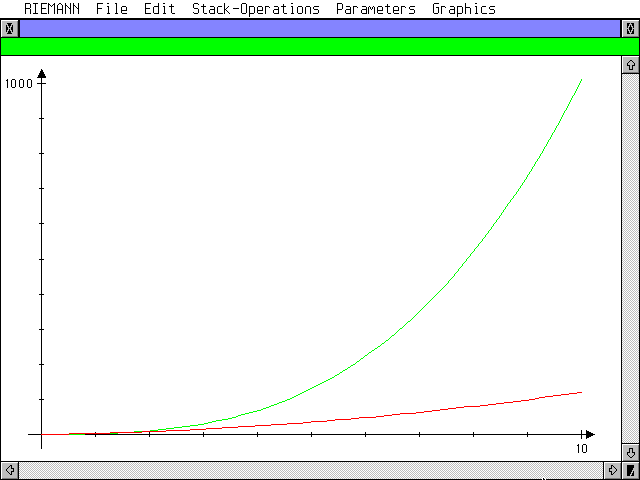 |
On the left : Let's compare TIMEALGO on two equal expressions: 1 + X + X² and 1 + X * ( 1 + X ). Both return N + N³. Why? RIEMANN evaluates and simplifies the expression passed as parameter. Have a look at the last lines: when typing the factorised expression, you get in return the expanded and reduced version. You have to go into the Parameters menu and unselect every automatic algebraic transformation. Furthermore, it should return 2N + N³ as there are two additions. Except that internally, the addition of several terms is reduced to one and only list, so the "+" appears only once. On the right : With the good settings, let's assign to S the calculation time for 1 + X + X², that's to say: S = N + N³. And let's assign to F the time calculation for 1 + X * ( 1 + X ), that's to say: F = 2N + N². Let's create an empty graph using 0 as expression. Then change the color and draw the graph of S, then again another color and add the graph of F. That's a way to compare the growths of the two time calculations according to N, the desired precision in numbers. (DIVOUT simplifies the quotient S/F if you want an analitic expression of the compared growth). |
A chaque nom, on peut associer une ou plusieurs propriétés. Dans l'exemple ci-contre, on crée avec PUT la propriété FIRSTNAME pour le nom NEWTON. Elle vaut ISAAC. Par la suite, si je demande avec GET ce que vaut FIRSTNAME pour NEWTON, il me répond ISAAC. Tout simple... Le nom peut être un nom sans signification, mais également le nom d'une fonction. C'est cette facilité qu'utilise REIMANN pour ses formules d'intégration ou de dérivation. A chaque fonction est associée une propriété de dérivation donnant la formule de sa dérivée. Si le nom n'a pas la propriété recherchée, GET renvoie simplement FALSE. |
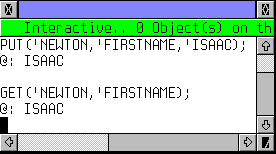 |
To each name can be associated one or more properties. In the example next, we create with PUT the property FIRSTNAME for the name NEWTON. It values ISAAC. Then, using GET, if I ask using for the FIRSTNAME for NEWTON, it returns ISAAC. So simple... The name can have no particular meaning, but can be a function name. This is used by RIEMANN for differentiate and integrate functions. For example, each function has its own derivative property that is used by DIF to compute the derivative. If a name has not the required property, GET returns FALSE. | 2
J'ai regroupé mes programmes dans un seul fichier source ALLMYPRG.RIE et, pour chacun, je crée la propriété HELP donnant une définition sommaire de ses paramètres. Ces définitions sont également intégrées au source. Je pourrai bien sûr utiliser GET pour ramener la propriété, mais on peut faire plus simple. |
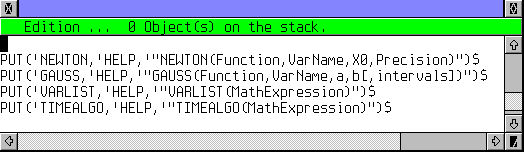 |
I grouped my programs into one single source file ALLMYPRG.RIE and, for each function, I create the HELP property giving a quick line description of the parameters. Those definitions are included into the source file. Then I could use GET to read back those properties, but I can do better. |
Ce fichier contient des définitions qui sont chargées automatiquement au démarrage de RIEMANN. Par défaut, il est vide. Mais vous pouvez voir qu'il charge un programme HELP que j'ai ajouté. Ce programme sera donc toujours disponible! Note : Attention à ne pas charger trop ce fichier AUTO car la lecture et la compilation d'un fichier source prennent un certain temps. |
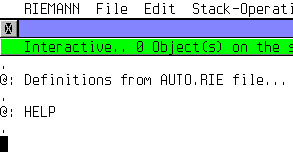 |
This file contains definitions that are automatically loaded at startup. The default file is empty. But you can see that I added a HELP program. So, this one will always be available now into RIEMANN. Note : be careful not to put too many things into the AUTO file as loading and compiling a source file can take some time. |
Le programme attend un paramètre, le nom d'une fonction.
HELP(GAUSS). |
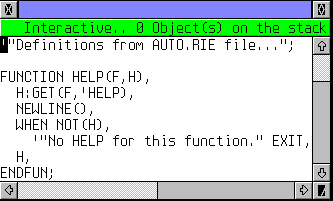 |
The program requires one parameter, the function name.
HELP(GAUSS). |
Je charge donc mes programmes et les propriétés à partir du fichier ALLMYPRG.RIE. Note :Si après ENDFUN vous terminez la définiton par "$", rien ne s'affiche au chargement. Si vous la terminez par ";", le nom de la fonction est affiché. C'est ce que j'ai fait ici, d'où la liste qui apparaît! Je demande ensuite l'aide du programme GAUSS avec HELP(GAUSS), et on me renvoie la définition de ses paramètres. Ce qui m'aide à lancer un calcul d'intégrale numérique. Pour finir, je demande l'aide sur INT, une fonction qui n'a pas cette propriété. Voyez le message. A travers ce système de propriétés, on peut étendre facilement les possibilités de RIEMANN: par exemple cette aide en ligne facile à mettre en oeuvre. |
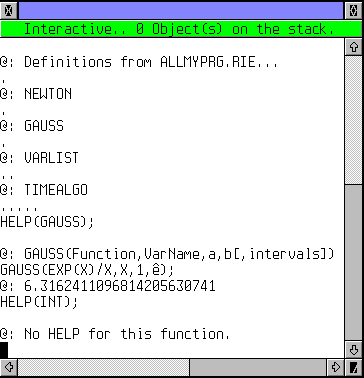 |
Let's load all my programs and properties from the file ALLMYPRG.RIE. Note :if after a ENDFUN you use the terminator "$", nothing appears when loading. If you use the terminator ";", then the function name is displayed. That's what I used there, this explains the list that you can see! Then, let's get the HELP line for the GAUSS function with HELP(GAUSS), you can see the parameters definiton appear. Thats helps to run an numerical integration with the correct parameter order. Then, let's do the same for INT, a function without this property. Read the message! Through this property system, one can easely extend the features of RIEMANN: for example, this little inline help so quickly set. |
 Voici le fichier contenant les programmes présentés sur cette page. Voici le fichier contenant les programmes présentés sur cette page.
|
|
 Here is the ZIP archive with every program listed on this page. Here is the ZIP archive with every program listed on this page.
|
RIEMANN est capable d'exporter un graphique au format GEM Metafile. Pour ce faire, dans la fenêtre 2D, sélectionnez METAFILE au lieu de SCREEN. Vous pouvez éventuellement donner un nom au fichier de sortie, par défaut ça sera "RIEMANN.GEM", j'ai choisi BUTERFLY.GEM pour mon exemple. Exécutez ensuite vos tracés, j'ai choisi ici une fonction paramétrique avec PARPLOT. Vous avez la possibilité de superposer plusieurs graphes. Pour que le fichier soit refermé proprement, n'oubliez pas de cliquer sur 'CANCEL GRAPH OUTPUT' qui met fin à la série des graphes. |
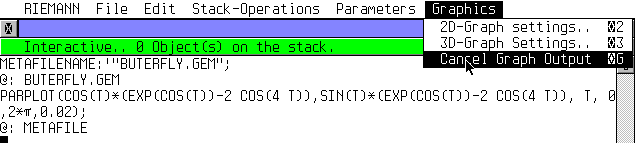 |
RIEMANN is able to export a graph to a GEM Metafile. In order to do that, select METAFILE instead of SCREEN in the 2D parameters. Then, you can give a name to your output file, it's BUTERFLY.GEM in this example. If you do not, the name will be RIEMANN.GEM by default. Finally, execute your graphic instructions, here I plot a parametric function with PARPLOT. You can add more than one graph. Don't forget to say that your graph is complete with the menu option 'Cancel graph Output' that properly closes the GEM file. | 2
On peut utiliser GEMVIEW qui charge ce type de fichier. On peut également utiliser ce programme pour une sauvegarde en IMG, GIF, TGA ou TIFF. Etrangement, cette conversion n'a pas toujours réussi! |
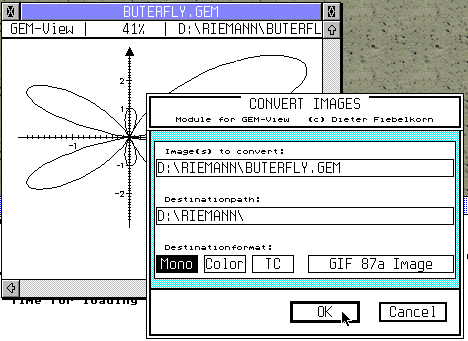 |
You can use GEMVIEW to display such a file. You can also make conversions of the metafile to a bitmap image as IMG, GIF, TGA or TIFF. Unexpectedly, the conversion didn't work each time. |
Si on désire aller vers les autres systèmes, ARABESQUE est parfait pour charger un metafile et le transformer en fichier EPS (Encaspulated PostScript), format bien plus répandu. Là encore, une tentative de conversion en IMG sous Arabesque a planté le programme, après une autre tentative, elle fut fructueuse. |
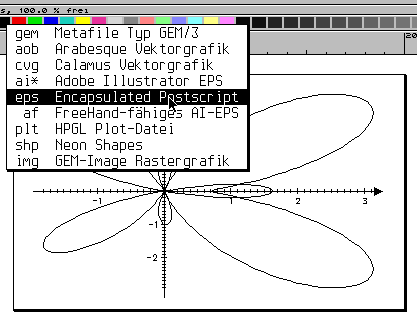 |
If you want to use your work on another system, then ARABESQUE is perfect to turn your metafile into a EPS (Encaspulated PostScript), widely spread. There again, converting the GEM to an IMG was not successful at first time, it hang the program. After a second try, it was a success. |
Finalement, sous Windows par exemple, l'installation de GhostScript permet de relire ce fichier et éventuellement de l'intégrer à d'autres documents. Ceci ouvre de larges possibilités selon les logiciels dont vous disposez, mais par exemple XnView permet la sauvegarde en PDF ainsi qu'en de multiples formats d'image. |
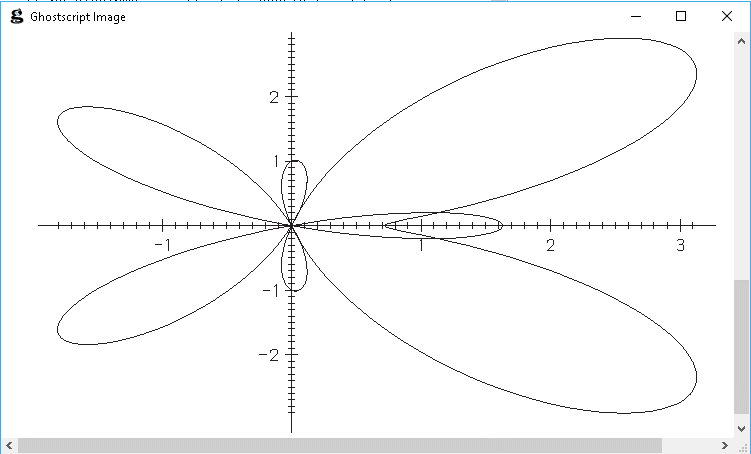 |
Finally, under Windows for example, after installing Ghostscript, you can open your file and eventually insert it into another document. This opens a wide range of possibilities according to the software you have. For example, XnView allows you to save this into a PDF or to many graphics formats. |